[2025年10月2日 更新]
都立入試数学の大問3は関数である。
その大問3の3問目(最終問題)でどのような問題が出るか。過去問を見たことのあるキミなら即答できるだろう。「面積比または等しい面積になる点Pの座標を求める」が圧倒的に多い。
◆過去16回のうち10回も
過去16年分の出題内容を見てみよう。
2025 三角形の面積が、他の三角形の2倍になる点Pのx座標
2024 三角形の面積が、他の三角形の3倍になる点Pのx座標
2023 三角形の面積が、他の三角形の2倍になる点Pのx座標
2022 線分比が3:1となる点Pのx座標
2021 三角形の面積が等しくなる点Pのx座標
2020 四角形が三角形の面積の4倍になる点Pのx座標
2019 三角形の面積が、他の三角形の2倍になる点Pのx座標
2018 直線が原点を通るための点Pの座標
2017 三角形の面積が、他の三角形の2/5倍になる点Pのx座標
2016 三角形の面積が、他の三角形の3倍になる点Pのx座標
2015 三角形の面積が、他の三角形の5倍になるときの線分の長さ
2014 三角形の面積が等しくなる点Pの座標
2013 三角形の面積が30cm2のとき点Pの座標
2012 三角形の面積が6cm2のとき点Pの座標
2011 三角形の面積比が3:2となる点Pの座標
2010 三角形の面積が49cm2のとき線分PRの長さ
過去10年だと7回も出題されている。
その7回も、2020年度を除けば三角形の面積どうしを比べる問題ばかりだ。
2次募集の入試問題でも同じ傾向がみられる。
都教委のWEBサイトで過去問を見られるので、ぜひ利用するといい。市販の過去問集には載っていない。
◆解き方は基本的に1パターン
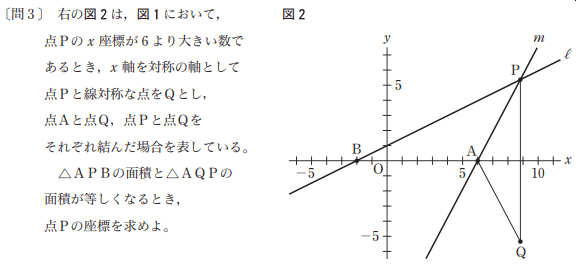
参照:都教育委員会HP
これは2018年度の都立高校2次募集の入試問題。
数学の大問3の3問目。直線lの式はy=1/2x + 1と判明している。
<解法>
△APQはx軸で面積二等分される。線分PQとx軸の交点を点Rとして、△APRの面積が△APBの半分になる点Rを考えればいい。
ABの長さは8と秒で出る。よってARの長さが4になればいい。
するとRのx座標が出るし、これは点Pのx座標と同じ。
考え方に気づけば1分間で解ける。
中2でも、すでに1次関数を学んでいるのであれば解ける問題。
中3のキミなら言わずもがな。
こういう問題を解けるように今まで訓練してきたかどうかだ。
Vもぎや過去問でそれは判明する。
ウチの塾生はきっと大丈夫だろう。

