[2026年2月27日 更新]
◆都立入試の1次方程式の傾向
2003年から2026年度までの大問1(4)、1次方程式とその解答をまとめた。
なお2002年度以前は、1次方程式のかわりに1次不等式が出されることもあった。
過去24回のうち、
( )のある式 12回
( )のない式 12回
解が正 13回
解が負 11回
解が整数 23回
解が分数 1回
また、
・( )の前の係数は必ず正の整数
・( )は1つの式に1カ所のみ。2017と2023年度以外はすべて右辺に( )がある
という傾向があった。
あくまで傾向ではあるが、知っていて損はない。
◆正答率は9割以上。しかし…
過去15年分の正答率を並べた。
2025 66.4%
2024 93.5%
2023 90.4%
2022 87.3%
2021 84.6%
2020 93.2%
2019 88.3%
2018 88.4%
2017 91.2%
2016 93.0%
2015 91.4%
2014 93.4%
2013 95.4%
2012 92.9%
2011 87.4%
例年90%を超えていたのだが、2018年度以降は90%を下回ることが増えた。
2018年度に正答率が急落した原因は間違いなく「解が分数だった」から。
過去問ではずっと整数解だったのに、急に分数で答えが出たら「あれ、間違えたかな?」と誰もが戸惑うだろう。
これからの受験生はラッキーだ。
分数の解の可能性があることを知っているためである。
今後も分数の解になるかもしれない、と心得ておこう。
なお「1/2」や「1/4」など、割り切れる小数(有限小数)で表せる解になるとは考えにくい。
解が「分数でも小数でも表せることになる」から。
例えば解が「1/4」なら、「0.25」でも正解になる。
「1/16」だったら「0.0625」である。
採点ミスを防ぐため、シンプルな解にしたほうがいいに決まっている。
だから
割り切れない無限小数が都立入試の答えとして出る可能性がある と思っておこう。
◆2025年度、分数式が出た
今年2025年度は、1次方程式に分数が使われた。
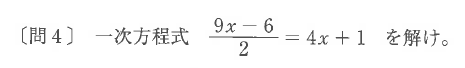
参照:都教育委員会Webサイト
過去にないパターンだったので、低学力層にとっては厳しい問題だったかもしれない。
正答率はガクンと下がり66.4%。
2026年度は( )も分数もなかったので、正答率は90%以上になるだろう。

