[2025年4月19日 更新]
都立高校入試の大問3は、関数問題が3つ出る。
その3つのうち、最も高正答率なのが1問目。
偏差値45以上を目指すなら絶対に取りたい問題だ。
今回はこの問題傾向と対策を伝える。
◆点の座標、直線の式、yの変域のどれか
都立入試では、2次関数と1次関数が交互に出るのは有名な話。
2次関数が2年連続で出ることはあるが、
・1次関数が連続で出たことはない
・2次関数が3年連続で出たことはない
ということは、次の2026年度入試では2次関数が出るのは間違いない。
とは言え、2次関数の問題を解く上で1次関数を使うことになる。1次関数を全くやらないのは自殺行為だ。
夏休みが終わるまでには1次関数を完璧にしておく必要がある。
もっともダイヤグラムの問題や、点Pが正方形の辺上を移動してできる三角形ABPの面積を求めるといった問題は都立入試で出ない。
グラフで考える問題に特化して勉強しよう。

過去21年分の大問3の1問目に何が出たかをまとめた。
1次関数の年は「直線の式」か「点の座標」のどちらかを求める問題。
2次関数の年は「yの変域」か「直線の式」を求める問題が出る。13回のうち「yの変域」が11回だ。
ただyの変域を求めるのではなく、わざわざaだbだと文字の種類を多くして分かりづらくするのが都立の特長。
以下の問題は2018年度のものである。
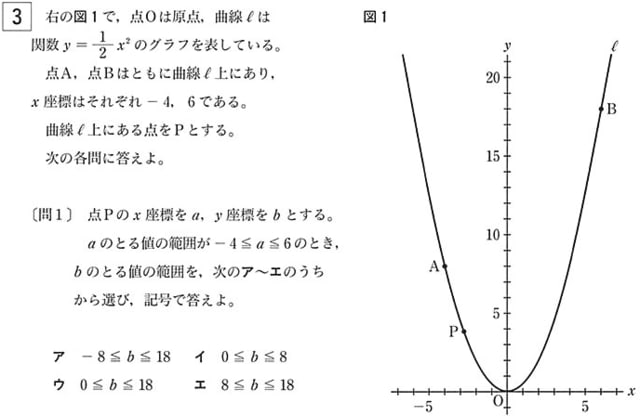
参照:都教育委員会サイト
わざわざx座標をa、y座標をbとしている。
やることは -4≦x≦6 の時のyの変域を答えるだけ。
もちろん、xの変域が負から正の数になるようにしてくる。yの最小値が0であることを答えさせるためだ。
慣れれば誰でも取れる。
絶対に落とさないよう、訓練しておくこと。
◆2026年度はどうなる?
2025年度は例年通り「1次関数の座標を求める」問題だった。
では2026年度では何が出るか。
過去の傾向だと2014年度からは1次関数・2次関数が交互に出ている。
それを信じれば99%で2026年度は2次関数だ。「yの変域」がくさい。
繰り返すが2002年度以降の都立入試で「2年連続で1次関数」は出たことがない。
私の塾では夏休みは1次関数を中心に、2次関数は少しだけ。
冬休みは2次関数と、円周角と相似の利用を中心に図形問題を扱うつもりだ。
2次関数の問題を解く際にはほぼ100%、1次関数の性質も使う。「1次関数だけ徹底的にやる」なんてことは恐ろしくてできない。
図形に比べて関数はヒントが多い。”補助線を思いつく”といったセンスがなくても解ける問題も多い。
2014~2024年度の大問3の33問中、正答率10%以下の問題は4問しか出ていない(2017,2018,2021,2024年度の3問目)
数学で80点以上を狙うなら、大問3の関数を3問とも取る。
これを意識しよう。
都立に入る! Twitter (X) そのときに必要な情報をこっそりと。ミンナニナイショダヨ
@toritsukoko

