[2023年11月24日 更新]
都立高校入試には傾向がある。とりわけ数学は顕著だ。
それを知っておけば、来年度は何が出題されるかが予想でき、対策しやすくなる。また一般入試と2次試験・分割後期募集では絶対に別の問題が出る。
今回は、大きく予想しやすい単元を3つ紹介する。
・確率or資料の整理
・1次関数or2次関数
・三角形 相似の証明or合同の証明
過去6年間の傾向は表のとおり。
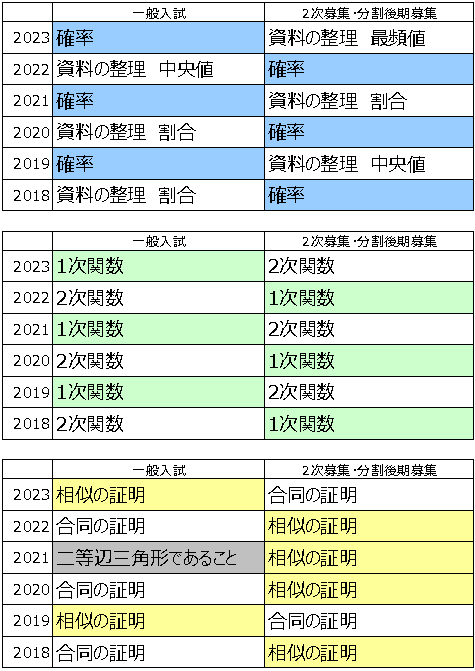
◆確率or資料の整理
大問1では確率か資料の整理の一方が出る。
出題傾向が分かりやすく、例外が起こっていない。
2024年度一般入試で出るのは間違いなく資料の整理だ。
資料の整理では割合、中央値、最頻値を聞かれている。
階級値を問われたことはない。例えば「身長150cm以上、155cm以下」の階級の階級値を答えられるだろうか。
このblog読者なら造作もない問題だが、世の公立中学の3年生では半数くらいしか答えられないだろう。
◆1次関数or2次関数
これも分かりやすい。隔年で2次関数が出ているので、2024年度は間違いなく2次関数だ。過去22年、1次関数が2年連続で出たことはない。
2年連続で2次関数が出たことはある。
もっとも2次関数の問題であっても、1次関数(直線)の式は使う。2次関数の知識だけでOKということではない。
◆相似の証明or合同の証明
これも相似と合同が交互に出される。
ただし2021年度入試はコロナ禍で出題範囲を削減した。
そのため今まで出たことがない、中2範囲の「二等辺三角形であることの証明」だった。ここ2年は法則が戻っている。
◆結論 2024年度はコレ
・資料の整理
・2次関数
・合同の証明
合同の証明は中2範囲だが、中3で学ぶ円周角の性質を用いた問題が出る可能性もある。
円周角の性質と三平方の定理の基本は身につけておけ。
うちの塾では飽きるくらい、円周角を求める問題を解かせている。

