[2021年5月19日 更新]
中間テストが終わってたりこれからだったりの時期。
1学期の数学はどの学年も代数が中心。中3なら平方根や2次方程式。
2学期でも2次関数がテスト範囲になるだろう。
関数は別だが、中学校の代数学では計算だけしておしまいという問題が多い。
慣れるだけで点がある程度取れるようになる。アタマを使わなくても解くだけならできちゃうのだ。
◆分かっていることを整理せよ
| <問> 生徒が長いすに座る。長いす1脚に4人ずつ座ると10人が座れない。 そこで、1脚に5人ずつ座ったところ全員が座れ、最後の長いすは3人になった。 長いすは何脚あったか求めよ。 |
定期テストではよく見るたぐいの問題だ。都立入試ではまず出ない。
もちろんこれは方程式を作って解くのだが、それが簡単でない子もいるだろう。
だったら図を描いてみたらいい。
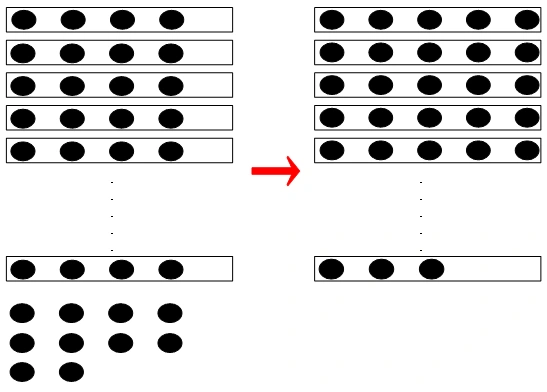
長方形が長いす、黒丸が人である。
2種類の座り方、どちらも長いすの数は同じである。もちろんその数は不明。
生徒の数も同じでありその数は不明である。
求めるのは長いすの数なので、長いすx脚と考えよう。
4人ずつ座るパターンの人数と、5人ずつ座るパターンの人数は同じ。
これをxを使って等式(方程式)にすればいい。
4人ずつ座る場合、
座った生徒数は4x、座れない生徒数が10。よって全生徒数は4x+10
5人ずつ座る場合、
生徒数は5xより2人少ない。よって生徒数は5x-2
これらは等しいのだから
4x+10 = 5x-2 が成り立つ。
あとはこれを解けばいい。
長いすの数なので、xは必ず正の整数である。
長いすが-10脚とか、8.4脚とかはあり得ない。
このように図を描くと、何が分かっていて、何が分かっていないのかが整理できる。
正しく問題文を読んでいないと(=見落としがあると)図をちゃんと書けないのだ。
まずは問題文に書いてあることを図にしてみると、ぐんと解きやすくなる。
道のり・速さ・時間の問題も同じだ。
これは関数でも図形問題でも同じ。
図やグラフを描くことで与えられた条件を整理でき、問題文の読み間違いをも防げる。
数値は図に書いてあるので、数字を覚えながら式を考えたり計算をする必要はない。計算だけに脳を使える。

