[2025年9月1日 更新]
都立入試共通問題の数学は、ありがたいことに図形や関数のグラフがほぼ正確に表されている。
よって、もともと書いてある図形や関数のグラフを利用すればいい。
◆いい加減な図の場合もある
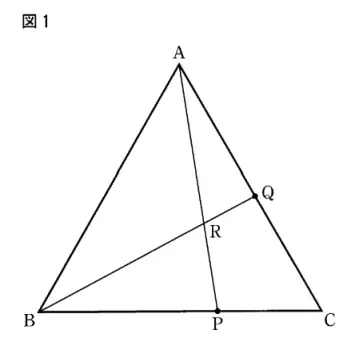
2008年度の都立入試で出た問題。
| ∠CBQ=? と∠BAP=a°とするとき,鋭角である∠ARQの大きさをaを用いた式で表せ。 |
さて、∠CBQは何度だと思うかな。(入試問題では ? に数字が置いてある)
せいぜい60度の半分の30度。辺AC上の点Qの位置を見て「30度より小さい」と考えられれば上出来だ。
しかし実は∠CBQ=40° としている。
このくらいの問題レベルなら図を書き直さなくても分かるかもしれない。
だが、これはどうだろう。
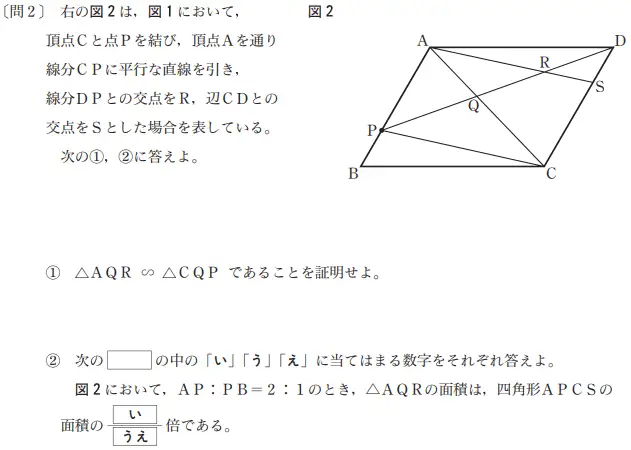
参照:都教育委員会HP
AP:PB=2:1 と書いてある。見えなくはないがもうちょっとPBが長くてもいいだろう。
ここで大事なのは、図を書くことで「与えられた条件(=仮定)を正しく読み取る」ということだ。
書いてある図だけでは仮定を読み取れない。
辺の長さの比や、PC//ASという最初に与えられている仮定から点Sの位置などを確かめながら図を書く。
そうすることで「今、判明していること」が整理できる。
また、知りたいのに分からない情報にも気づける。
辺の長さの比、角度、平行・垂直などの位置関係などだ。
図を書く時間がもったいないという奴もいるが、そういう奴に限って大事な情報を見逃している。
図を書く。それもちょっと大きめに。
これは試験当日、いきなりできることではない。今から過去問を解く際に練習しておくこと。
◆放物線は左右対称ならいい
2次関数(中学校では2乗に比例する関数のみ)のグラフはうまく描くのが厄介だ。
だがこれも練習次第でコツが分かってくる。
比例定数は1/2か1/4しか出ない。詳しくは過去記事を読まれたい。
「左右対称に描く」というポイントだけは絶対に外さないようにしよう。
<過去記事:都立高校入試数学の法則<12> 比例定数は2種類のみ>

